Note

This is a TIL (“Today I Learned”) post. I expect it to be useful to my future self and maybe to others, but it is meant to be a quick, informal way to capture something I learned rather than a polished presentation.

The Puzzle

Today I encountered a puzzling phenomenon: my model’s loss curve appeared to be bimodal. I was working to eliminate sources of randomness in order to reproduce another interesting finding, and I saw that the loss usually followed one curve, but sometimes followed a second curve, and always followed one of the two:

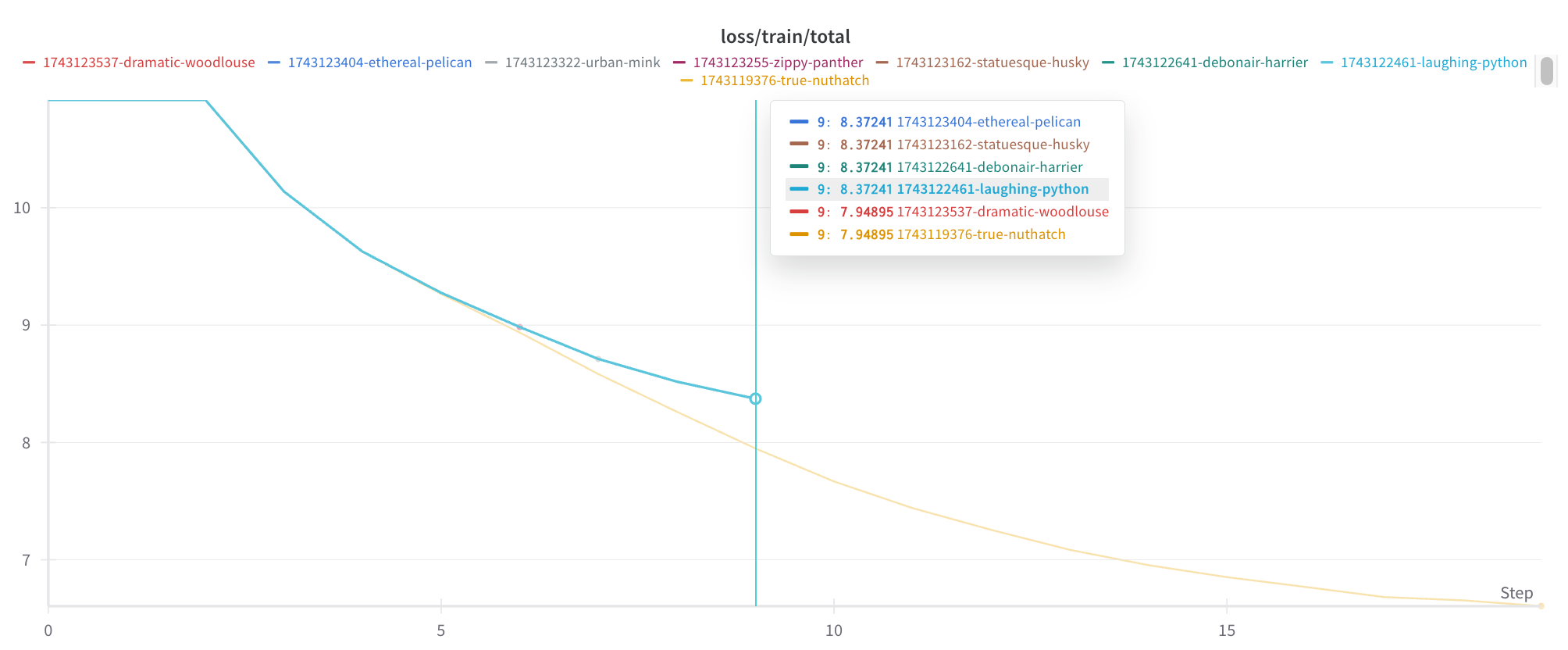
The Solution

I had decided to move on when a third curve appeared:

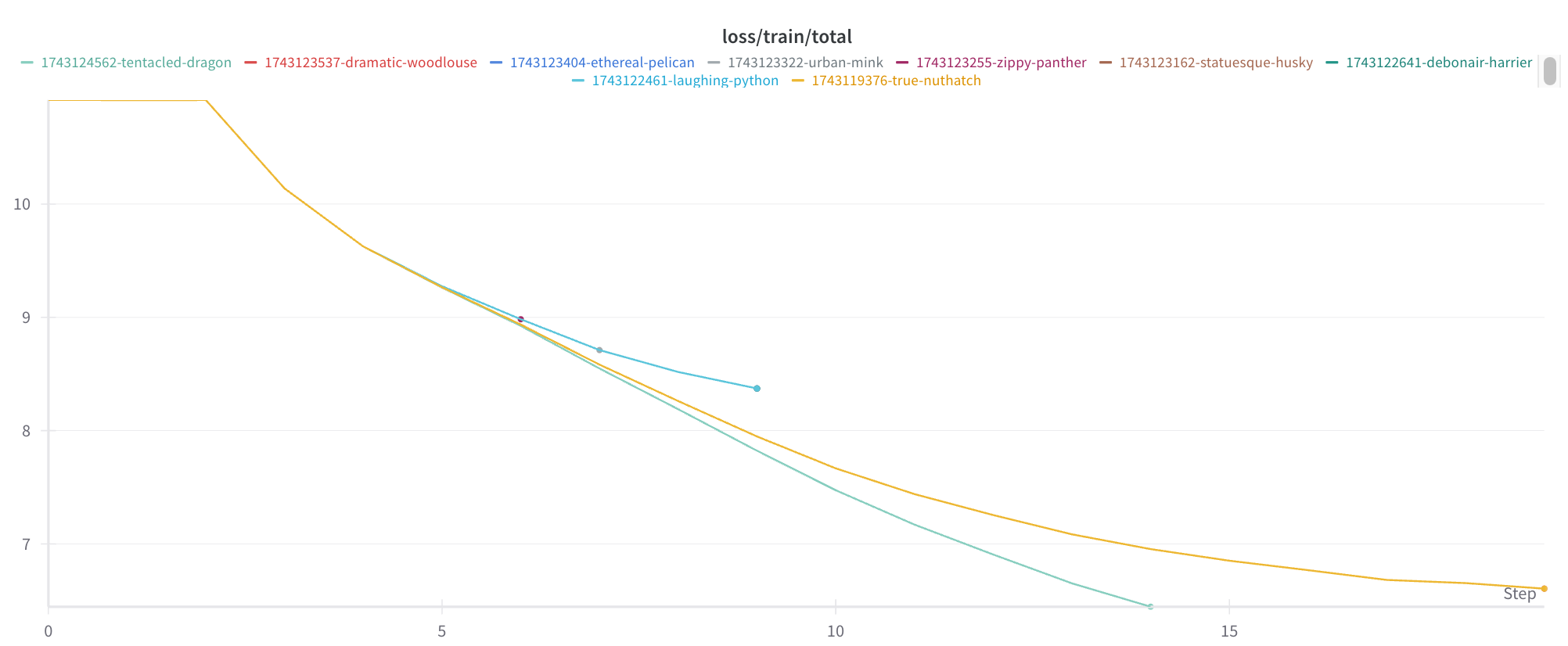
I then realized that the difference between the two initial sets of runs was coming from their max duration.

Why would a run’s max duration affect the loss curve at intermediate stages of training? Because the learning rate was scheduled to decay over the course of the run after an initial warmup. When the run is longer, it decays more slowly:

Note

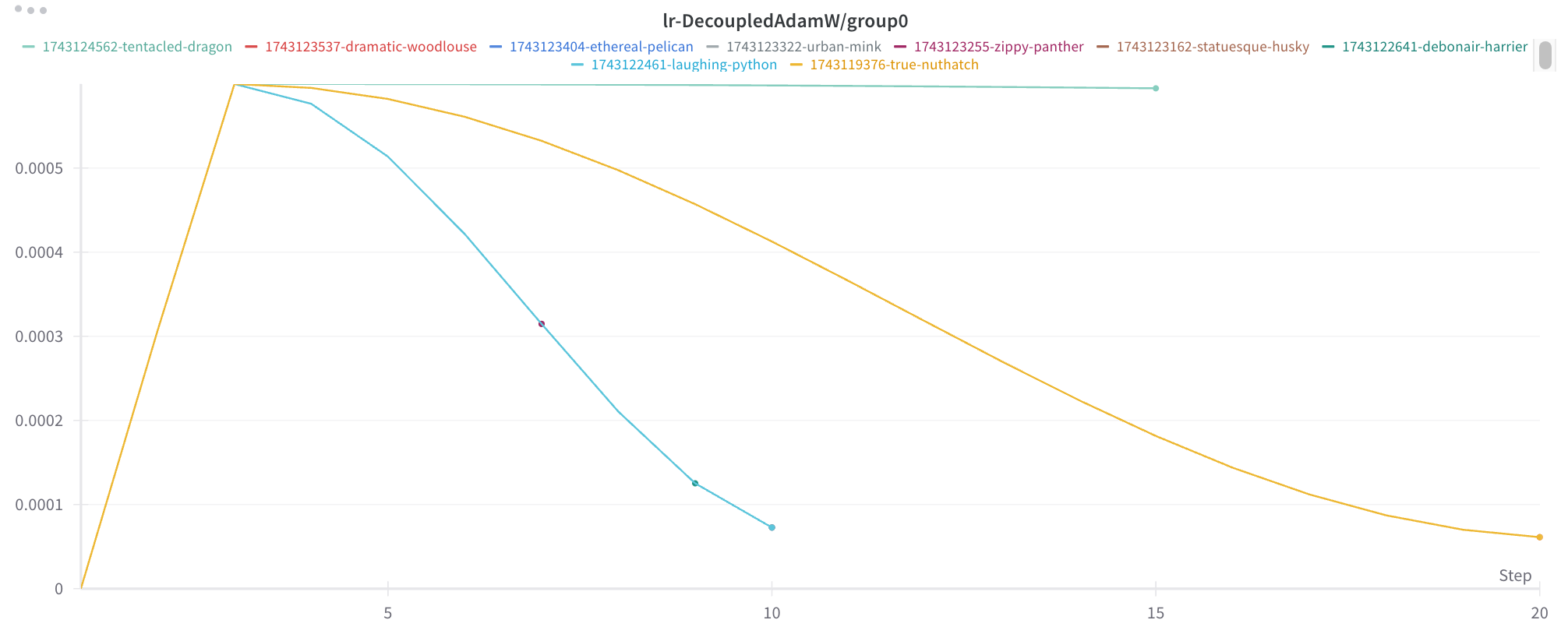
This was my LLM-Foundry learning rate scheduler configuration:

scheduler:
  name: cosine_with_warmup
  t_warmup: 200000tok
  alpha_f: 0.1

Why It Matters

It is important to realize when the learning rate depends on the run max duration for at least two reasons:

Reproducibility requires leaving max_duration fixed even for results early in training.
The optimal learning rate schedule hyperparameters will depend on max_duration.

How to Deal with the Interaction Between Learning Rate and Max Duration

There are two ways to deal with this interaction between learning rate and max duration:

Eliminate it, by using a constant learning rate or a schedule that is independent of max_duration (e.g. a cyclic schedule).
Account for it, for instance by settling on a max_duration first and then tuning learning rate schedule hyperparameters.

My understanding is that cosine decay is commonly used in LLM training, so it is important to be aware that changing the max duration under this approach will affect the entire training process.